Βαθιά μάθηση- Η επαναστατική δύναμη της ποσοτικής οικονομίας που εξημερώνει την «κατάρα της διάστασης»

Η βαθιά μάθηση έχει τη δυνατότητα να μετασχηματίσει ριζικά την ποσοτική οικονομία, επιτρέποντας στους οικονομολόγους να εξερευνήσουν νέα εδάφη, να απαντήσουν σε πιο σύνθετα ερωτήματα και να σχεδιάσουν πιο αποτελεσματικές πολιτικές.

 
Συναρπαστικές νέες προοπτικές για την ποσοτική οικονομική

 
Ερευνητικό έγγραφο από το National Bureau of Economic Research εξερευνά τον τρόπο με τον οποίο η βαθιά μάθηση μπορεί να βοηθήσει στην επίλυση σύνθετων μαθηματικών προβλημάτων στην οικονομική επιστήμη. Οι συγγραφείς επισημαίνουν ότι η βαθιά μάθηση προσφέρει μια ελπιδοφόρα προσέγγιση για τον έλεγχο της κατάρας της διάστασης (curse of dimensionality), ένα πρόβλημα που περιορίζει την ικανότητα των οικονομολόγων να λύνουν πολύπλοκα οικονομικά μοντέλα. Επιπλέον, το έγγραφο υποστηρίζει ότι η βαθιά μάθηση δεν είναι μια “μαγική” λύση, αλλά μάλλον μια πιο αποτελεσματική γεωμετρική μέθοδος που μπορεί να βοηθήσει στην καλύτερη αναπαράσταση του χώρου των δυνατών καταστάσεων ενός μοντέλου.

 
Η βαθιά μάθηση και η επίλυση Δυναμικών Μοντέλων Ισορροπίας

Η βαθιά μάθηση υπόσχεται να επεκτείνει δραματικά την κατηγορία των δυναμικών μοντέλων ισορροπίας (ΔΜΙ) που μπορούμε να διαχειριστούμε και τα σχετικά με την πολιτική ερωτήματα που μπορούμε να απαντήσουμε. Αυτό οφείλεται κυρίως στην ικανότητά της να εξημερώνει την κατάρα της διάστασης   σε πολλές περιπτώσεις.

Ας δούμε αναλυτικότερα πώς η βαθιά μάθηση επηρεάζει την ικανότητα των οικονομολόγων να λύνουν ΔΜΙ:

• Υπερπαραμετροποίηση: Τα αλγοριθμικά μοντέλα μηχανικής μάθησης, συμπεριλαμβανομένων των βαθιών νευρωνικών δικτύων, συχνά έχουν πολύ περισσότερες παραμέτρους από τα δεδομένα. Αυτό τους επιτρέπει να προσαρμόζουν πολύπλοκες συναρτήσεις των χώρων κατάστασης υψηλής διάστασης που συναντώνται στα ΔΜΙ.
• Κανονικοποίηση: Η κανονικοποίηση είναι ζωτικής σημασίας για την καθοδήγηση των αλγορίθμων μηχανικής μάθησης στην επιλογή λύσεων με επιθυμητές ιδιότητες. Στα βαθιά νευρωνικά δίκτυα, η κανονικοποίηση επιτυγχάνεται με διακριτικούς τρόπους, όπως μέσω του σχεδιασμού του δικτύου, του αλγορίθμου βελτιστοποίησης, ή του θορύβου στα δεδομένα. Η κανονικοποίηση διασφαλίζει ότι τα μοντέλα δεν υπερπροσαρμόζονται στα δεδομένα.
• Αναπαραστάσεις: Τα μοντέλα μηχανικής μάθησης συχνά μετασχηματίζουν τον χώρο κατάστασης σε μια αποδοτική αναπαράσταση που συλλαμβάνει τα βασικά χαρακτηριστικά του ΔΜΙ.
• Συγκέντρωση Μετρήσεων: Πολλές μέθοδοι μηχανικής μάθησης εστιάζουν στα “τυπικά σύνολα” των μεταβλητών κατάστασης, τα οποία γίνονται ολοένα και πιο αντιπροσωπευτικά (και μικρότερα σε σχετικό όγκο) του χώρου λόγω της συγκέντρωσης μετρήσεων.
• Βελτιστοποίηση Υψηλής Διάστασης: Τα εργαλεία μηχανικής μάθησης αξιοποιούν αλγορίθμους βελτιστοποίησης υψηλής διάστασης, ικανούς να λύνουν προβλήματα με πολλές παραμέτρους και να κανονικοποιούν μη κυρτούς στόχους.

Η επιτυχία των βαθιών νευρωνικών δικτύων οφείλεται κυρίως στη μεταβολή της γεωμετρίας στον χώρο αναπαράστασης. Αυτή η μεταβολή επιτυγχάνεται με:

• Μάθηση Χαμηλής Διάστασης Αναπαραστάσεων: Τα βαθιά νευρωνικά δίκτυα μπορούν να μάθουν χαμηλής διάστασης αναπαραστάσεις, όπως αυτές που χρησιμοποιούνται σε μεθόδους όπως η προσέγγιση διαταραχών.
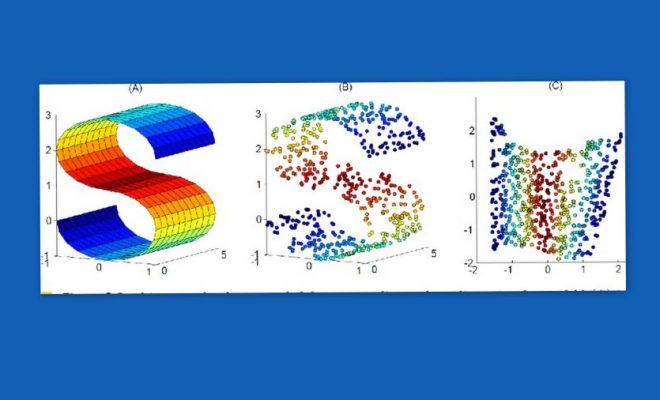
• Υπόθεση Πολλαπλότητας: Η υπόθεση πολλαπλότητας υποδηλώνει ότι τα πραγματικά δεδομένα, συμπεριλαμβανομένων εκείνων από ΔΜΙ, συγκεντρώνονται σε πολλαπλότητες χαμηλής διάστασης.
• Μεταβιβασιμότητα: Η χρήση βαθιών αναπαραστάσεων επιτρέπει την επαναχρησιμοποίηση υπολογισμών σε διάφορες εκδόσεις ενός ΔΜΙ.

Η βαθιά μάθηση υπόσχεται να επαναμορφώσει τα ΔΜΙ που χρησιμοποιούμε για την ανάλυση οικονομικών φαινομένων. Παράλληλα, η νέα γενιά υλικού διευρύνει περαιτέρω τις δυνατότητές μας. Ενώ χρειάζεται προσοχή και βαθύτερη κατανόηση της θεωρίας αναπαράστασης και φαινομένων όπως η διπλή κάθοδος, η βαθιά μάθηση ανοίγει συναρπαστικές νέες προοπτικές για την ποσοτική οικονομική.

 
Διαφορές μεταξύ παραδοσιακών και Βαθιάς Μάθησης Μεθόδων Λύσης Δυναμικών Μοντέλων Ισορροπίας

Οι πηγές του εγγράφου επισημαίνουν διάφορες βασικές διαφορές μεταξύ των παραδοσιακών μεθόδων λύσης Δυναμικών Μοντέλων Ισορροπίας (ΔΜΙ) και των μεθόδων βαθιάς μάθησης:

• Υπεπαραμετροποίηση: Τα παραδοσιακά μοντέλα χρησιμοποιούν συναρτήσεις προσέγγισης με λίγες παραμέτρους για να αποφευχθεί η υπερπροσαρμογή. Αντίθετα, οι αλγόριθμοι Μηχανικής Μάθησης, συμπεριλαμβανομένων των Νευρωνικών Δικτύων (ΝΔ), συχνά έχουν πολύ περισσότερες παραμέτρους από δεδομένα. Αυτό επιτρέπει στα ΝΔ να προσαρμόζονται σε περίπλοκες συναρτήσεις σε χώρους κατάστασης υψηλής διάστασης.
• Κανονικοποίηση: Λόγω της υπεπαραμετροποίησης, οι μέθοδοι Μηχανικής Μάθησης βασίζονται σε διάφορες μορφές κανονικοποίησης για να επιλέξουν λύσεις με επιθυμητές ιδιότητες. Η κανονικοποίηση μπορεί να προκύψει από τον σχεδιασμό του ΝΔ, τον αλγόριθμο βελτιστοποίησης, ή τον θόρυβο στα δεδομένα.
• Αναπαραστάσεις: Τα ΝΔ μετασχηματίζουν τον χώρο κατάστασης σε μια αποτελεσματική αναπαράσταση που συλλαμβάνει τα βασικά χαρακτηριστικά του ΔΜΙ. Αυτό επιτυγχάνεται μέσω αλλεπάλληλων γεωμετρικών μετασχηματισμών των χαρακτηριστικών των δεδομένων.
• Συγκέντρωση Μέτρου: Οι μέθοδοι Μηχανικής Μάθησης συχνά εστιάζουν σε “τυπικά σύνολα” μεταβλητών κατάστασης, τα οποία γίνονται ολοένα και πιο αντιπροσωπευτικά (και μικρότερου σχετικού όγκου) λόγω του φαινομένου της συγκέντρωσης μέτρου.
• Βελτιστοποίηση Υψηλής Διάστασης: Τα ΝΔ χρησιμοποιούν αλγόριθμους βελτιστοποίησης υψηλής διάστασης που μπορούν να λύσουν προβλήματα με πολλές παραμέτρους και να κανονικοποιήσουν μη κυρτές συναρτήσεις στόχους.

Εν κατακλείδι, ενώ οι παραδοσιακές μέθοδοι προσπαθούν να προσεγγίσουν τις λύσεις ΔΜΙ με βάση προκαθορισμένες συναρτήσεις, η βαθιά μάθηση εστιάζει στην εύρεση αποτελεσματικών αναπαραστάσεων του χώρου κατάστασης μέσω αλλεπάλληλων γεωμετρικών μετασχηματισμών. Αυτό επιτρέπει στα ΝΔ να διαχειρίζονται την “κατάρα της διάστασης” και να λύνουν ΔΜΙ πολύ μεγαλύτερης πολυπλοκότητας.

 
Η βαθιά μάθηση στην ποσοτική οικονομία: Μια προοπτική μετασχηματισμού

Η βαθιά μάθηση (deep learning) εμφανίζεται ως μια επαναστατική δύναμη στην ποσοτική οικονομία, προσφέροντας εργαλεία για την αντιμετώπιση της «κατάρας της διάστασης» (curse of dimensionality). Αυτή η κατάρα, που αναφέρεται στην εκθετική αύξηση της πολυπλοκότητας καθώς αυξάνονται οι διαστάσεις ενός προβλήματος, έχει περιορίσει για χρόνια τους οικονομολόγους σε μοντέλα με λίγες μεταβλητές.

Η βαθιά μάθηση, μέσω των νευρωνικών δικτύων (NΔ), υπόσχεται να «δαμάσει» αυτή την κατάρα. Τα ΝΔ, αποτελούμενα από πολλαπλά στρώματα, μπορούν να προσεγγίσουν πολύπλοκες συναρτήσεις με ακρίβεια, ακόμα και σε προβλήματα με πολλές διαστάσεις.

Η δύναμη των ΝΔ έγκειται στην ικανότητά τους να μαθαίνουν αποτελεσματικές γεωμετρικές αναπαραστάσεις του χώρου των δεδομένων. Μετασχηματίζουν τον αρχικό χώρο σε έναν πιο “φιλικό” χώρο, όπου η προσέγγιση γίνεται ευκολότερη.

Τα πλεονεκτήματα της βαθιάς μάθησης στην ποσοτική οικονομία είναι πολλά:

• Επέκταση του εύρους των μοντέλων: Η βαθιά μάθηση επιτρέπει στους οικονομολόγους να εργαστούν με μοντέλα με πολύ περισσότερες μεταβλητές, ανοίγοντας νέους ορίζοντες στην έρευνα.
• Βελτιωμένη ακρίβεια: Τα ΝΔ μπορούν να επιτύχουν εξαιρετικά ακριβή αποτελέσματα, ιδιαίτερα σε περιοχές του χώρου των δεδομένων που έχουν μεγάλη σημασία για την οικονομική ανάλυση.
• Αυτοματοποίηση και ευελιξία: Η βαθιά μάθηση αυτοματοποιεί πολλές από τις διαδικασίες που απαιτούνται για την επίλυση των μοντέλων, καθιστώντας την έρευνα πιο αποτελεσματική.

Η εφαρμογή της βαθιάς μάθησης σε διάφορους τομείς της ποσοτικής οικονομίας ήδη αποδίδει καρπούς:

• Δυναμικός προγραμματισμός: Τα ΝΔ χρησιμοποιούνται για την επίλυση σύνθετων προβλημάτων βελτιστοποίησης, tanto σε διακριτό όσο και σε συνεχή χρόνο.
• Μοντέλα ετερογενών πρακτόρων: Η βαθιά μάθηση συμβάλλει στην αντιμετώπιση της πολυπλοκότητας που εισάγουν οι ετερογενείς πράκτορες, προσφέροντας λύσεις για μοντέλα με αλληλεπιδράσεις και αβεβαιότητα.
• Εκτίμηση μοντέλων: Η βαθιά μάθηση επιταχύνει τη διαδικασία εκτίμησης των μοντέλων, επιτρέποντας την ανάλυση μεγάλων συνόλων δεδομένων.

Ενώ η βαθιά μάθηση ανοίγει νέους δρόμους στην οικονομική έρευνα, είναι σημαντικό να υιοθετηθεί με σύνεση.

• Η ερμηνευσιμότητα των ΝΔ παραμένει πρόκληση.
• Η επιλογή της κατάλληλης αρχιτεκτονικής δικτύου και η σωστή ρύθμιση των παραμέτρων του είναι κρίσιμη για την επιτυχία της εφαρμογής.

Παρόλα αυτά, η βαθιά μάθηση έχει τη δυνατότητα να μετασχηματίσει ριζικά την ποσοτική οικονομία, επιτρέποντας στους οικονομολόγους να εξερευνήσουν νέα εδάφη, να απαντήσουν σε πιο σύνθετα ερωτήματα και να σχεδιάσουν πιο αποτελεσματικές πολιτικές.

Info 1

Διαβάστε το πλήρες έγγραφο εργασίας εδώ . aei.org

 
Info 2

curse of dimensionality

Η κατάρα της διάστασης αναφέρεται σε διάφορα φαινόμενα που προκύπτουν κατά την ανάλυση και την οργάνωση δεδομένων σε χώρους υψηλών διαστάσεων που δεν συμβαίνουν σε περιβάλλοντα χαμηλών διαστάσεων όπως ο τρισδιάστατος φυσικός χώρος της καθημερινής εμπειρίας.